Die numerische Modellierung der festen Erde
Prozesse in der festen Erde sind für die direkte Beobachtung unzugänglich. Die Auswirkung der Massenumverteilung und Deformation der festen Erde kann jedoch mithilfe von Satellitenbeobachtungen und Beobachtungen an der Erdoberfläche erfasst werden. Die Messergebnisse beinhalten meist eine Überlagerung von vielen Prozessen. Numerische Modelle sind ein nützliches Werkzeug, um Prozesse der festen Erde vereinfacht abzubilden und zu separieren. Diese vereinfachte Abbildung der Natur beinhaltet eine mechanische Beschreibung der festen Erde.
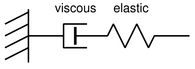
Die feste Erde erstreckt sich von ihrer Oberfläche bis zum Kern und beinhaltet im Allgemeinen nicht die Ozeane, die Atmosphäre oder Eisschilde. Die mechanischen Eigenschaften der festen Erde werden durch einen kontinuumsmechanischen Ansatz beschrieben. Das heißt, die Erde wird in kleine Volumenelemente aufgesplittet, für die die entsprechenden Materialeigenschaften beschrieben werden. In guter Näherung verändern sich die Materialeigenschaften wie Dichte oder Elastizität nur mit der Tiefe, was auf eine sphärisch symmetrische Struktur führt. Generelle physikalische Prinzipien werden verwendet, um die Wechselwirkung der Volumenelemente zu beschreiben. Integration über das Volumen des Erdkörpers definiert dann ihre Antwort auf eine wirkende Kraft. Für die in dieser Sektion betrachteten Oberflächen- und Gezeitenkräfte sind die Lithosphäre und der Erdmantel von Hauptinteresse. Je nachdem auf welcher Zeitskala die Prozesse ablaufen, kann ein elastisches oder viskoses Materialverhalten angenommen werden.
Referenzen:
Klemann, V. (2024 online): Gravito-viscoelastodynamics. - In: Sideris, M. G. (Ed.), Encyclopedia of Geodesy, (Encyclopedia of Earth Sciences Series (EESS)), Cham : Springer International Publishing, 1-6; doi.org/10.1007/978-3-319-02370-0_141-1
Die elastische Reaktion auf Oberflächenkräfte kann adäquat durch lineare Übertragungsfunktionen, Green'sche Funktionen, parametrisiert werden, die auf einer radial symmetrischen Dichte- und Elastizitätsverteilung im Erdinnern beruhen. Die jeweilige Erdstruktur muss für kleinräumige Prozesse gegebenenfalls angepasst werden.
Für die Untersuchung von Oberflächendeformationen, die durch saisonale Änderungen im terrestrischen Wasserkreislauf oder in der Atmosphäre bewirkt werden, wurde in Abhängigkeit von der jeweiligen elastischen Kruste (Erdstruktur) die Deformation der Erdoberfläche berechnet. Dazu wurde für eine lateral variierende Krustenstruktur in erster Näherung an jedem Gitterpunkt ein eigener Satz von Green'schen Funktionen gerechnet. Diese beschreiben in Abhängigkeit von der Entfernung zur Laständerung die Reaktion der festen Erde.
Numerisch aufwendiger ist es, laterale Variationen in den elastischen Eigenschaften, konsistent zu modellieren. Diese treten vor allem an den tektonischen Plattengrenzen zu Tage und beeinflussen das Deformationsverhalten. Dichtevariationen obwohl auch von Belang beeinflussen dagegen das Deformationsverhalten weniger. Im Erdmantel kommt ein weiteres Phänomen hinzu, die Anelastizität, Sie besagt, dass sich die elastischen Moduln mit der Dauer der Beanspruchung verringern, das Material sich als stärker deformiert. Ähnlich wie in der Kruste sind die anelastischen Eigenschaften von Ort zu Ort verschieden. Sie sind stark temperaturabhängig, ihre Bestimmung ist damit eng mit Untersuchungen über die Dynamik des Erdmantels verknüpft. (Siehe auch Department 2 "Geophysik")
Referenzen:
Tanaka, Y., Klemann, V., Martinec, Z. (2024): An estimate of the effect of 3D heterogeneous density distribution on coseismic deformation using a spectral finite-element approach. - In: Freymueller, J.T., Sánchez, L. (eds) X Hotine-Marussi Symposium on Mathematical Geodesy. HMS 2022. International Association of Geodesy Symposia, vol 155. Springer, Cham. p 103-111, doi.org/10.1007/1345_2023_236
Huang, P., Sulzbach, R., Klemann, V., Tanaka, Y., Dobslaw, H., Martinec, Z., Thomas, M. (2022): The influence of sediments, lithosphere and upper mantle (anelastic) with lateral heterogeneity on ocean tide loading and ocean tide dynamics. - Journal of Geophysical Research: Solid Earth, 127, 11, e2022JB025200. doi.org/10.1029/2022JB025200
Huang, P., Sulzbach, R., Tanaka, Y., Klemann, V., Dobslaw, H., Martinec, Z., Thomas, M. (2021): Anelasticity and lateral heterogeneities in Earth's upper mantle: impact on surface displacements, self‐attraction and loading and ocean tide dynamics. - Journal of Geophysical Research: Solid Earth, 126, 9, e2021JB022332. doi.org/10.1029/2021JB022332
Tanaka, Y., Klemann, V., Martinec, Z. (2019): Surface Loading of a Self-Gravitating, Laterally Heterogeneous Elastic Sphere: Preliminary Result for the 2D Case. - In: IX Hotine-Marussi Symposium on Mathematical Geodesy, (International Association of Geodesy Symposia ; 151), 157-163. https://doi.org/10.1007/1345_2019_62
Dill, R., Klemann, V., Martinec, Z., Tesauro, M. (2015): Applying local Green's functions to study the influence of the crustal structure on hydrological loading displacements. - Journal of Geodynamics, 88, p. 14-22.| doi.org/10.1016/j.jog.2015.04.005
Für Prozesse wie die glazial isostatische Anpassung GIA muss neben dem elastischen auch das viskose Verhalten des Erdmantels berücksichtigt werden. Das viskoelastische Verhalten bewirkt, dass sich während des letzten glazialen Maximums also vor etwa 20.000 Jahren, der Erdboden in den vergletscherten Gebieten um bis zu einem Kilometer gesenkt hatte und sich der Boden nach dem Abschmelzen der Eisschilde immer noch hebt.
Siehe hierzu auch: Glazial isostatische Anpassung
Referenzen:
Bagge, M., Klemann, V., Steinberger, B., Latinovic, M., Thomas, M. (2021): Glacial-isostatic adjustment models using geodynamically constrained 3D Earth structures. - Geochemistry Geophysics Geosystems (G3), 22, 11, e2021GC009853. doi.org/10.1029/2021GC009853
Tanaka, Y., Hasegawa, T., Tsuruoka, H., Klemann, V., Martinec, Z. (2015): Spectral-finite element approach to post-seismic relaxation in a spherical compressible Earth: application to gravity changes due to the 2004 Sumatra-Andaman earthquake. - Geophysical Journal International, 200, p. 299-321. doi.org/10.1093/gji/ggu391
Cambiotti, G., Klemann, V., Sabadini, R. (2013): Compressible viscoelastodynamics of a spherical body at long timescales and its isostatic equilibrium. - Geophysical Journal International, 193, 3, p. 1071-1082. http://doi.org/10.1093/gji/ggt026
Spada, G., Barletta, V. R., Klemann, V., Riva, R. E. M., Martinec, Z., Gasperini, P., Lund, B., Wolf, D., Vermeersen, L. L. A., King, M. (2011): A benchmark study for glacial isostatic adjustment codes. - Geophysical Journal International, 185, 1, 106-132; doi.org/10.1111/j.1365-246X.2011.04952.x
Klemann, V., Martinec, Z., Ivins, E. R. (2008): Glacial isostasy and plate motion. - Journal of Geodynamics, 46, 3-5, p. 95-103. doi.org/10.1016/j.jog.2008.04.005